Mathematics can be profoundly intricate. While the base components may appear to be simple, the fundamental philosophy can be intensely profound, even baffling at times. In this discussion, we will traverse a spectrum of topics, from prime numbers to the concept of infinity. Ready yourself for a mental exercise; we’re about to dig into 25 Outstanding Mathematical Concepts That Will Stretch Your Thinking!
The equator rope
 Source: abc.net.au, Image: pexels (public domain)
Source: abc.net.au, Image: pexels (public domain) If you wrapped a rope around the equator of the Earth so that it was tightly hugging the ground, you would only need to add about 6.3 meters of rope in order for the entire thing to hover 1 meter above ground level (all the way around the Earth). This counterintuitive result works no matter how big the sphere is. The most simple way to explain this is to remember that circumference is equal to diameter times pi. This means that if you want to make the rope hover 1 meter above the Earth, you only need to increase the diameter by 2 meters (1 meter on each end of the globe). Therefore, you would only need to increase the circumference of the rope by 2 x pi meters (6.28318530718 meters).
Hippasus of Metapontum
 Source: esoterx.com, Image: https://commons.wikimedia.org (public domain)
Source: esoterx.com, Image: https://commons.wikimedia.org (public domain) The man who proved that irrational numbers existed was murdered for it. His name was Hippasus of Metapontum, and it happened around 520 BC. Pythagoras and many Greek mathematicians of the time believed that all numbers were integers, or whole. It was when Pythagoras was performing his famous triangle calculations (Pythagorean theorem) that he stumbled across the square root of two. To make a long story short, he allegedly tried to keep his finding a secret and flipped out when Hippasus published it.
Munchausen numbers
 Source: zach.se
Source: zach.se Apart from making some assumptions about 0^0, 3435 is the only number besides 1 where you can split each digit up, raise it to its own power, sum it all together, and get the same number back. Basically, 3^3 + 4^4 + 3^3 + 5^5 = 3435 Note: 438579088 also works if you assume that 0^0 = 0. These are called Munchausen numbers.
The decimal representation of the 7th's
 Image: https://pixabay.com (public domain)
Image: https://pixabay.com (public domain) The decimal representations of the 7th’s are the same set of numbers being repeated except always starting from a different point. 1/7 = 0.142857142857… and 2/7 = 0.285714285714… and 3/7 = 0.428571428571…
Binary finger counting
 Source: mathisfun.com, Image: https://pixabay.com (public domain)
Source: mathisfun.com, Image: https://pixabay.com (public domain) If you use binary, you can count to 1023 on your fingers.
10!
 Source: reddit.com
Source: reddit.com There are exactly 10! seconds in 6 weeks. It’s easier to see this when you break it down as such: 6 * 7 * 24 * 60 * 60 = 6 * 7 * (8 * 3) * (3 * 2 * 10) * (1 * 3 * 4 * 5) = 6 * 7 * 8 * 9 * 2 * 10 * 1 * 3 * 4 * 5 = 10!
Graham's number
 Source: ibmathresources.com, Image: https://pixabay.com (public domain)
Source: ibmathresources.com, Image: https://pixabay.com (public domain) Graham’s number is so big that if you wrote every digit as small as you possibly could, it would still take up more space than is available in the observable universe. In fact, if you could hold all of the digits in your head your brain would collapse into a black hole (due to the astronomical density of neural connections you would require).
Repeating decimals
 Image: https://pixabay.com (public domain)
Image: https://pixabay.com (public domain) Any repeating decimal can be written as a fraction over an equivalent number of 9’s (as the repeating part). For example, .456456456… would be 456/999
Shuffling cards
 Source: qi.com, Image: https://www.pexels.com (public domain)
Source: qi.com, Image: https://www.pexels.com (public domain) Every time you randomly shuffle a deck of 52 cards, you have almost certainly arranged them in an completely unique order. What we mean by this is that in the entire history of mankind, nobody has ever shuffled a deck in the same way. How? Well, there are 52! ways that you can order the deck (52*51*50…) This leads to 8.0658 x 10^67 possibilities. In comparison, the universe is only 1 x 10^18 seconds old. Even if you shuffled one deck every second since the big bang…you’d still fall miserably short.
The Klein Bottle
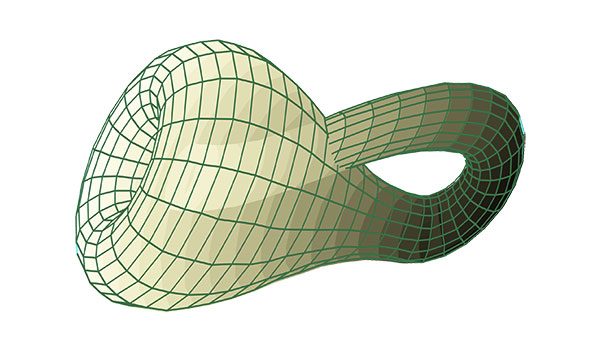 Source: math.union.edu
Source: math.union.edu If you take two Möbius strips and extend the edges so that they connect (in effect glueing them together), you create a Klein Bottle. This “bottle” is an example of a non-orientable surface. Basically, it exists only in 4 dimensions, but can be loosely represented in 3. Like the Möbius strip, it has only 1 surface, but no edges. It’s pretty trippy.
The Frivolous Theorem of Arithmetic
 Source: mathworld.wolfram.com, Image: https://pixabay.com (public domain)
Source: mathworld.wolfram.com, Image: https://pixabay.com (public domain) The Frivolous Theorem of Arithmetic states that due to being infinite, the vast majority of natural numbers are very, very large.
What lies between 0 and 1
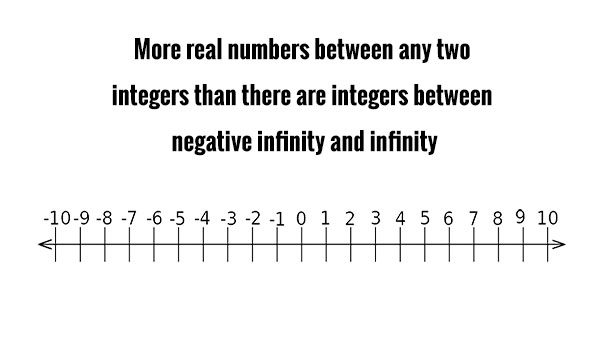
There is an infinite amount of numbers between 0 and 1 (and 1 and 2, etc). For example, ½, ⅓, ¼, and you can just keep on going.
Non-computable numbers
 Source: igoro.com, Image: http://www.pixnio.com (public domain)
Source: igoro.com, Image: http://www.pixnio.com (public domain) Almost all real numbers are irrational. Even more, most irrational numbers aren’t even computable. And to really boggle your mind, every single number you’ve ever seen in your life is computable, including infinitely repeating numbers like pi (because you can create an algorithm to compute it). So, to put things simply, there is an infinite amount of numbers out there that we will never see (in fact…most of them) because we have no way of computing those numbers. In some sense, they are the “dark matter” of mathematics. We know they are there and that they constitute the unspeakable majority of numbers, but we have no way of reaching them. Note: Chaitin’s constant is an example of non-computable number, but unfortunately…it’s not computable.
The different types of infinity
 Source: math.brown.edu, Image: https://pixabay.com (public domain)
Source: math.brown.edu, Image: https://pixabay.com (public domain) Although the integers are infinite, there are infinitely more real numbers than integers. How can that be if the integers are already infinite? It’s because there are two types of infinity…countable and uncountable. Integers are infinitely countable, whereas real numbers are not (because they also include the irrational numbers). So this leads to some crazy conclusions. The number of positive integers (0, 1, 2, …) is exactly the same as the number of positive and negative integers combined (…, -3 , -2, -1, 0, 1, 2, 3, …). Although these two infinite sets are equal, they are both smaller than the infinite set of real numbers. In fact, there are infinitely more numbers between just two random integers (0 and 1 for example) than there are in the entire infinite set of integers!
The normal numbers
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com A normal number is basically an irrational number which doesn’t have any more of a given digit than another. So, for example, in the number 4.56856948576434… every single digit should appear roughly an equal number of times all the way out to infinity. Although there is rough proof to show that most real numbers are normal, and we suspect that numbers like pi and e are normal, we have still not been able to show it.
The Transcendental Numbers
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com Although almost every single real and complex number is transcendental (as opposed to algebraic, which is basically any number that is the root of a polynomial), there are only a few that are known, primarily because it is really hard to prove that a number is transcendental. The best known transcendental numbers are e and pi.
The lonely prime
 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain) Every single prime number all the way through to infinity is odd. Except for 2.
The effect of infinity on probability
 Image: https://pixabay.com (public domain)
Image: https://pixabay.com (public domain) The concept of infinity has some crazy effects on probability. If you were to randomly select a real number, the probability of it being rational (1, 2, ¾, 78/56, …) is 0. This goes back to the fact that the irrational numbers are uncountably infinite, whereas the rational numbers are countably infinite. And, countable infinity over uncountable infinity is 0.
.999... = 1
 Image: https://commons.wikimedia.org (public domain)
Image: https://commons.wikimedia.org (public domain) .999… is equal to 1. By this point your mind is probably so boggled with the concept of infinity that you will probably just accept whatever we tell you, but we’ll prove it. You know that .333… is equal to ⅓ and .666… is equal to ⅔. ⅓ + ⅔ = 1 and .333… + .666… = .999…. Another way to think of this is that if .999… doesn’t equal 1, there would have to be some number between .999… and 1. Which, thanks to the concept of infinity, there isn’t.
The Dirichlet Function
 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com According to the Dirichlet function, between any two irrational numbers there is a rational number. The crazy part? There are infinitely more irrational numbers than rational numbers (as we previously established). So…how could every two irrational numbers have a rational number between them? You would expect to run out of rational numbers. But infinity just doesn’t behave the way we expect it to.
Euler's Identity
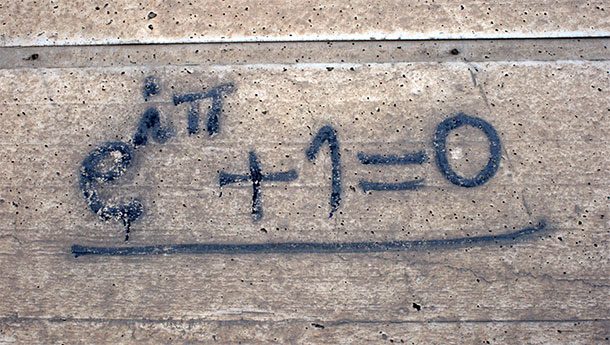 Source: mathworld.wolfram.com
Source: mathworld.wolfram.com Euler’s Identity is often cited as an example of mathematical beauty. It is e^(pi*i)+1=0. It contains 5 of the most fundamental mathematical constants 0,1, e, pi, and i. Also, three of the basic arithmetic operations occur exactly once: addition, multiplication, and exponentiation. Benjamin Peirce, a noted mathematician once said after proving it in a lecture, “the identity is absolutely paradoxical; we cannot understand it, and we don’t know what it means, but we have proved it, and therefore we know it must be the truth.”
The Monty Hall Problem
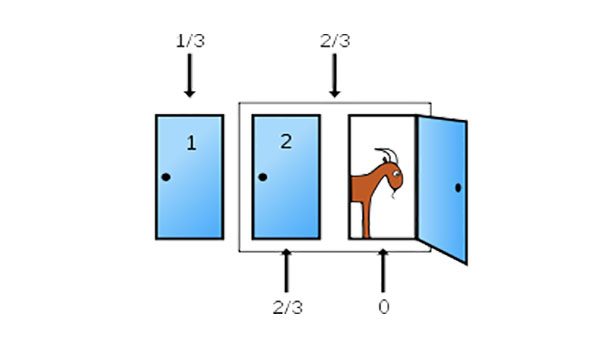 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain) The Monty Hall problem is a famous example of how probability can be counter-intuitive. Let’s say that on a game show there are three doors. Behind one of them is a car while the other two are hiding goats. You choose to open door 1. The host, however, knows what is behind the doors. He opens door 3 to reveal a goat. Now he asks you if you would like to change your choice to door 2. What do you do? The answer is that you should change your choice. Why? Because by changing to door 2 you have a ⅔ chance of winning the car while staying on door 1 you have a roughly ⅓ chance. The best way to visualize this counter-intuitive solution is to increase the number of doors. Let’s say now that there are 100 doors. You pick door 37. The host now opens all the doors to reveal goats except for door 83. Do you want to change your pick from 37 to 83? Or would you stay on 37? The fact is that your chances of winning the car will increase significantly by switching to door 83.
The difference between 1 million and 1 billion
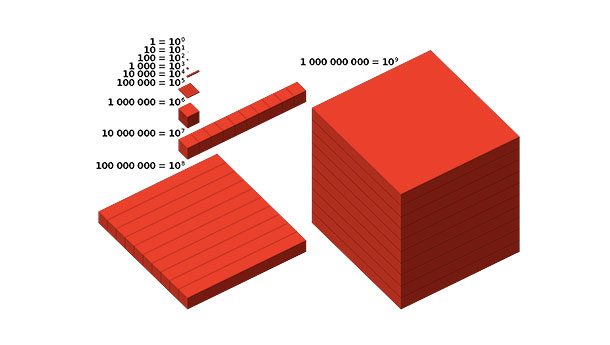
One million seconds is about 11 and a half days. One billion seconds is just under 32 years.
The Pigeonhole Principle
 Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain)
Source: mathworld.wolfram.com, Image: https://commons.wikimedia.org (public domain) If you have 2 types of socks in your drawer and you randomly grab 3 without looking, you are guaranteed to have a matching pair. While for some people this is obvious, for others it can be harder to grasp. It is based on something called the pigeonhole principle. Basically, if you have n types of something, then you need to randomly choose n+1 of that thing in order to get a match. So, if you have 5 different types of socks in your drawer and you randomly grab 6 of them…you’re guaranteed to have a match. This can be great for getting dressed in the dark!
The sum of all positive integers from 1 to infinity
 Source: see below, Image: https://commons.wikimedia.org (public domain)
Source: see below, Image: https://commons.wikimedia.org (public domain) Now, get ready for possibly the most mind boggling thing you’re ever going to hear in your entire life. If you add up all of the positive integers from 1 to infinity…what do you get? Did you guess -1/12? Because that’s the right answer. We know. This sounds absolutely ridiculous and to some extent it is. Why? Because adding anything up to infinity is impossible and sure to yield ridiculous results. To make things even crazier for you, this result is actually very well known in physics, particularly string theory. In fact, if you still can’t believe this, we suggest that you watch this video by physicists Tony Padilla and Ed Copeland from the University of Nottingham. They explain the craziness better than we can – https://www.youtube.com/watch?v=w-I6XTVZXww.
Note: the result stems largely from the fact that infinity defies our expectations. Infinity isn’t a number, it’s a concept. Things like addition and subtraction don’t work the same when you involve infinity (kind of how physics doesn’t work the same when you’re standing in the middle of a black hole).
More information: it is also worth looking into Ramanujan summation and Grandi’s series:
https://en.wikipedia.org/wiki/Ramanujan_summation
https://en.wikipedia.org/wiki/Grandi’s_series
Another resource:
http://www.bradyharanblog.com/blog/2015/1/11/this-blog-probably-wont-help
Lists Going Viral Right Now
Photos: Featured Image: https://commons.wikimedia.org (public domain), 20. max pixel, 16. Tttrung, Klein bottle2, CC BY-SA 4.0, 11. Mehran Moghtadaei, PP 1280×1024, CC BY-SA 3.0, 10. Stephen J. Brooks (talk), Algebraicszoom, CC BY 3.0, 6. Judy Breck via flickr , CC BY-SA 2.0 , 5. Quinn Dombrowski from Chicago, USA, Euler’s Identity Graffito, CC BY-SA 2.0, 3. Cmglee, Visualisation 1 billion, CC BY-SA 3.0,



























