Though mastering mental math might not be crucial in today’s world, it’s still an incredibly beneficial skill to have. In this piece, we’ll delve into a range of tactics and thought patterns to aid you in retaining, calculating, and managing numbers mentally and on paper. Some tips are of a general nature, whereas others address specific scenarios or real-life instances such as calculating tips. This article presents 25 simple mental math tricks that are sure to impress you!
Divisibility by 3

To see if a number is divisible by three, add up the digits. If the sum is divisible by three, so is the number. Note: this also works for 9.
Switching percentages
x% of y is the same as y% of x. This means that if 2% of 50 is too hard to figure out, you can just flip it – 50% of 2. That’s a lot easier.
Multiplying by 11

To multiply a 2 digit number by 11 just add the digits together and stick the answer between them. For example 42*11 would be 4 + 2 = 6. Now put the 6 between the 4 and the 2 to get 462.
Note: Don’t forget to carry the 1. To give another example, 58*11 would be 5 + 8 = 13. You can’t just put the 13 between the 5 and the 8 though. That would give 5138, which is obviously wrong. You need to carry the one by adding it to the 5. So it would be 638.
Multiplying by 5

If you need to multiply a number by 5 it may be easier to half it and then multiply by 10. For example, 315*5 would be 315 / 2 = 157.5 Now just move the decimal over to multiply by 10 and get 1575.
Approximating a square root

To approximate a square root, do the following. Find the next lower perfect square. Add it to your number. Now divide by the square root of the lower perfect square. And now divide again by 2. Sounds hard? Here’s an example. Take 31. The next lowest perfect square is 25. So 31 plus 25 is 56. Now divide by the square root of 25. So 56 / 5 = 11.2 Now divide by 2 to get 5.6
Binomial Theorem for squaring
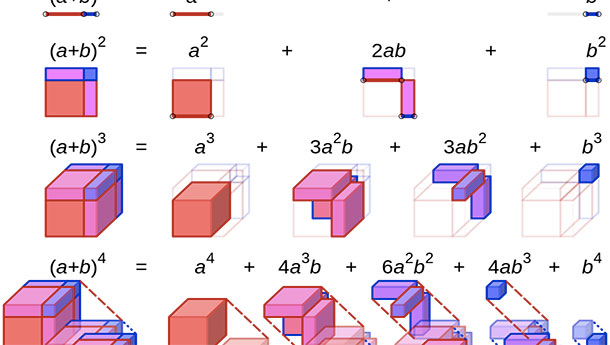
Use the binomial theorem (a + b)^2 = a^2 + 2ab + b^2 to square numbers. For example 55^2 could be (50 + 5)^2. This means that 50*50 + 50*5*2 + 5*5 = 2500 + 500 + 25 = 3025.
Divisibility by 8

To see if a number is divisible by 8, check the last three digits. If they are divisible by 8, then the number is divisible by 8. For example, 3423024 would be divisible by 8 because 024 / 8 = 3
Tipping

To figure a tip just move the decimal one place to the left in order to get 10%. Then either add half of what you have left to get 15% or double it for 20%. For example, if the bill is $43.21 then $4.32 is 10%. Half of $4.32 is $2.16 so if you want 15% just add that on. It would give you $4.32 + $2.16 = $6.48. Getting 20% is even easier because you just double it. $4.32*2 = $8.64. So if you’re feeling generous then $8.64 would constitute a 20% tip.
Salary calculations

To calculate your annual salary, just take your hourly wage, double it, and add 3 zeros. Let’s say you are making $8 per hour. Just double that for $16 and then add three zeros for $16,000.
Convert between Celsius and Fahrenheit

To approximate conversions between Celsius and Fahrenheit just multiply by 2 and add 30 (going from C to F). Do the reverse to go from F to C (subtract 30 and divide by 2).
Divisibility by 4

To see if a number is divisible by 4 just look at the last two digits. If they are divisible by 4 then the entire number is divisible by 4. So 23746316 would be divisible by 4 because 16 is divisible by 4.
FOIL method for multiplication
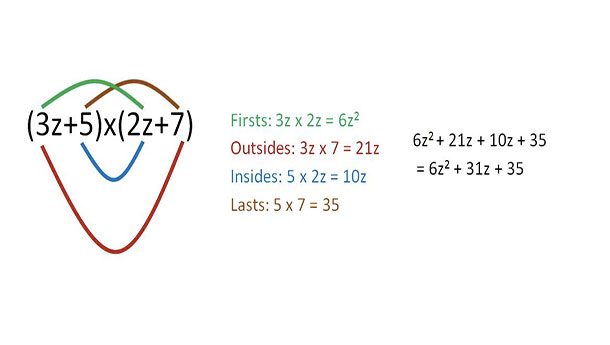
To multiply two numbers together, use the FOIL method (first, outer, inner, last). For example, 25*37 would be (20)(30) + (5)(30) + (7)(20) + (5)(7) = 925.
Note: this is exactly what you do when you multiply on paper, it’s just easier to visualize the FOIL method in your head.
Calculating percentages

To calculate the percentage of a number (that isn’t 10%) just find 1% first and then multiply it. So, for example, 3% of 528 would be 528*.01 = 5.28 (move the decimal two places left). Now just multiply by 3 to get 15.84
Multiply by rounding

This works especially well if one of the numbers is already nice and round (ends in 0). Just round off the other number, multiply, and adjust the result accordingly. For example, if you want to calculate 18*30 you don’t need the FOIL method we did earlier (because 30 is already nice and round). Just do 20*30 which is 600 and then subtract two 30s for 540.
Divisibility by 6

To check if a number is divisible by 6 you need to combine two divisibility rules (twos and threes). If it is divisible by both 2 and 3 then it is divisible by 6. We did divisibility by 3 already but just in case…even numbers are divisible by 2.
Decimal representations of the 11ths

The decimal representation of the 11ths can be done by multiplying the numerator by 9 and just repeating it. For example, 1/11 = .09090909…. and 2/11 = .18181818… etc
Squaring numbers that end in 5

To square any double digit number that ends in 5, just put 25 at the end and multiply the first number by the following digit. So, for example, 45^2 would be 2025 because 5 is the next digit above 4 so 4*5 = 20. Now just put a 25 on the end for 2025.
Converting 9ths into decimals

The decimal representations for the ninths are just the numerator repeated. For example 1/9 = .1111111… and 2/9 = .2222222… This is also one of the proofs used to show that .999999… = 1. (since 9/9 = .99999…)
The add/subtract method for squaring

For squaring numbers, one possible trick is to add/subtract from the number until you get two numbers you can easily multiply. Then add the difference of the number you added/subtracted. To give an example, 46^2 could be 42*50 because 46 – 4 = 42 and 46 + 4 = 50. So 42*50 would be 2100. Now square the number you added/subtracted so 4^2 = 16. Now add 16 to get 2116.
Rule of 72

72 divided by the interest rate will give you a rough estimate of how many years it would take to double your money (rule of 72).
Adding in your head

To do mental addition, it is much easier to work from left to right rather than the way you do on paper (right to left). This is because your brain naturally recognizes and remembers numbers starting at the left. For example, to do 376 + 581, add 300 + 500 to get 800. Now add on 70 + 80, which is 150. This brings the total to 950. Then add on the 7 to get 957. Basically, break the addition down into smaller parts from left to right. Another advantage of this is that you’ll gradually home in on the solution. So, if you only want an approximation you don’t have to wait until you finish the problem to figure out what order of magnitude you are working with (hundreds, thousands, etc)
Subtracting in your head

For mental subtraction, the idea is similar to addition. Work left to right, but there is an extra trick that you need to be aware of (hint: it involves rounding). Let’s say you want to do 632 – 487. First, add 3 in order to round 487 up to the nearest 10, so 490. Now, the problem becomes 632 – 490. This is much easier. 632 – 400 is 232. Now subtracting 90 you get 142 (it’s 10 more than subtracting 100). From there, just remember to add back the 3 from the beginning. This gives you 145.
The Subtraction Method

Another trick for multiplying numbers that are easily rounded up (usually ending in 8 or 9), is to use the subtraction method. To do this, you round up the number and then subtract. For example, 49*16 would be 50*16. This is much easier to solve. Since 100*16 is 1600, you can half that to get 800. Now just remember to subtract what you initially rounded. So, since you rounded 49 up to 50, that was 1*16, which is what you have to subtract. That gives 800 – 16 which is 784.
Handling equations
Remember that you can do anything you want to an equation as long as you do it to both sides. Also, you can do whatever you want to a term, as long as you are multiplying it by one. Keep in mind that 1 has infinite forms (2/2, (x-4) / (x-4), etc).
Convert Miles and Kilometers

To convert miles to kilometers, you can get a pretty close estimate by adding 60%. The fastest way to do this is to add 50% and then 10%. For example. 60 miles in km would be the following: 60*.5 = 30 and 60*.1 = 6. Now, 30 + 6 = 36. Add this to 60 to get 96 km. To go from kilometers to miles, just subtract 40%. You can do this by subtracting 50% and then adding 10%. So to get 350 km in miles subtract half of 350. That gives you 175. Now add back 10% of 350 which is 35. This leaves you with 210. Note: keep in mind that these are very rough estimates. The bigger your numbers get, the more error there will be.
Lists Going Viral Right Now
Image Credits: 1-2. Public Domain, 3. Shutterstock, 4-9. Public Domain, 10.
Endarrt (talk) via en.wikipedia.org CC BY-SA 3.0, 11-14. Public Domain, 15. Enoch Lau via commons.wikimedia.org CC BY-SA 3.0, 16. Public Domain, 17. Nick Youngson via thebluediamondgallery.com CC BY-SA 3.0, 18. Global Panorama via Flickr CC BY-SA 2.0, 19. Public Domain, 20. Cmglee via commons.wikimedia.org CC BY-SA 3.0 , 21-25. Public Domain,



























